SIT 212, TP4

Mme Charlotte LANGLAIS - Dept. Mathematical and Electrical Engineering

Simulation de signaux et briques de transmission - TP4 : Synthèse et implantation matérielle d’une chaîne de transmission numérique sur circuit reconfigurable

Introduction

Cette séance de Travaux Pratiques est une initiation à la conception de circuits intégrés numériques. Elle permet de découvrir les différentes étapes de la description d’une architecture en VHDL (langage dédié à l’électronique) jusqu’au test sur circuit reconfigurable FPGA (Field-Programmable Gate Array), le tout avec un outil professionnel, Vivado du fondeur de circuits Xilinx. Le second objectif de ce TP est d’illustrer certaines notions de communications numériques, telles que le choix d’un mapping efficace, ou l’influence du bruit sur la transmission, tout en concevant un émetteur et un récepteur à partir d’une description matérielle. Cette séance de TP est donc complémentaire des séances de SIT213 dédiées à l’implémentation d’une chaîne de transmission en logiciel avec un processeur généraliste.

Les grandes étapes de la conception d’un circuit sur FPGA sont les suivantes :

• conception de l’architecture du circuit sous forme de blocs/modules organisés hiérarchiquement,
• description des modules qui peut se faire par l’intermédiaire de langages de description matérielle (VHDL ou Verilog entre autres) ou d’outils de CAO proposant des modules déjà conçus paramétrables,
• simulation fonctionnelle de chaque module,
• intégration des modules pour réaliser le circuit complet,
• simulation du circuit complet,
• synthèse du circuit transformant la description hiérarchique en liste de composants logiques (portes élémentaires connectées),
• simulation post-synthèse pour vérifier que le modèle synthétisé est conforme au modèle initial,
• implantation physique qui consiste à traduire la liste précédente en liste de composants de la technologie cible (un FPGA donné par exemple), puis à les placer sur la cible matérielle et à les router,
• simulation post-placement-routage pour vérifier la conformité des performances,
• configuration(programmation) du circuit puis test du circuit sur carte.

Chacune des étapes de simulation et de test peut déclencher un retour en arrière plus ou moins important en cas d’échec.

En pratique, vous suivrez un flot simplifié, en bénéficiant du travail préparatoire des enseignants :

Phase 1 Description et simulation de modules combinatoires simples

• une description « à trous » en VHDL est fournie et doit être complétée sur la base de la description qui en est donnée ;
• chaque module VHDL est ensuite simulé et corrigé si nécessaire.

Phase 2 Simulation du circuit complet

Le circuit complet est simulé et le résultat analysé. Les résultats de simulation sont comparés aux résultats théoriques.

Phase 3 Synthèse, placement, routage et test du circuit complet

• le flot de « compilation » matérielle doit être paramétré puis lancé ;
• le résultat de ce flot est analysé puis testé sur carte.

Présentation de la chaîne de transmission

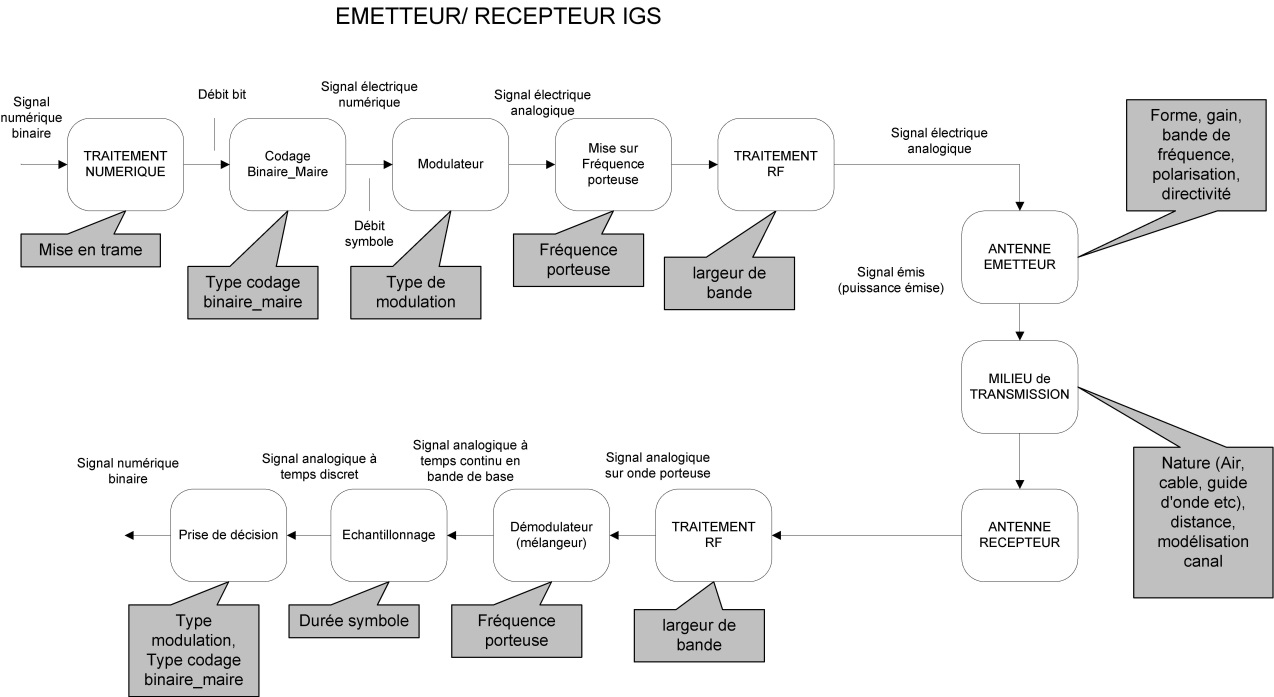
Afin d’illustrer le flot de conception de circuit numérique, nous choisissons de concevoir un émetteur et un récepteur d’une chaîne de transmission numérique en bande de base. La chaîne de transmission générique est représentée sur la figure ci-dessous. Elle contient l’ensemble des traitements numériques et analogiques nécessaires à la transmission de l’information sur un milieu de transmission.

TP4 - Chaîne de transmission. Les boites grisées contiennent les paramètres/caractéristiques des fonctions associées

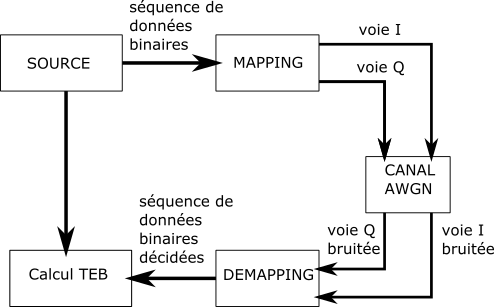
Dans ce TP, nous souhaitons émuler une transmission numérique en bande de base sur un circuit numérique reconfigurable de type FPGA. Le schéma simplifié de la transmission, telle qu’elle sera émulée sur le circuit FPGA, est donné figure ci-dessous. Contrairement à une transmission réaliste, toutes les fonctions émission, canal et réception sont placées sur la même carte. Dans la « vraie vie », l’émetteur et le récepteur ne sont pas co-localisés. Ce type de prototype matériel permet, par exemple, de vérifier les performances d’une modulation pour des taux d’erreurs binaires extrêmement bas du fait de la rapidité des opérations réalisées par le FPGA.

TP4 - Chaîne de transmission simplifiée.

La source génère une séquence pseudo-aléaoire de bits en série. Le bloc mapping convertit la séquence binaire en deux signaux qui représentent la voie I et la voie Q du symbole complexe de modulation de type MAQ16 (Modulation d'Amplitude en Quadrature à 16 états). Le canal à bruit blanc additif gaussien (Additive White Gaussian Noise, AWGN) permet de modéliser une source de bruit thermique ainsi que la perte en espace libre. Il est paramétré à partir du rapport signal-sur-bruit (signal to noise ratio, SNR). Dans notre contexte, comme la puissance du signal en entrée du canal ne varie pas, c'est la variance du bruit généré par le canal \(\sigma_b^2\) qui est modifiée, telle que \(SNR = 10 \textrm{log}_{10} \frac{1}{2 \sigma_b^2}\). En sortie, les deux voies I et Q sont donc bruitées. Le demapping a pour rôle d'appliquer la règle du maximum de vraisemblance afin de décider des bits qui ont été émis. En sortie, on obtient une séquence de données binaires décidées, qui va pouvoir être comparée à la séquence qui a été émise grâce au bloc de calcul du taux d'erreurs binaires (TEB).

Présentation du circuit à concevoir : MAQ16

Fonctions principales

Le circuit à concevoir permet d'émuler une chaîne de transmission simplifiée en bande de base qui comprend un émetteur intégrant une modulation MAQ16, un canal à bruit blanc additif gaussien et un récepteur qui réalise la détection binaire puis calcule le taux d'erreurs binaires correspondant. Le choix du rapport signal-à-bruit se fait grâce aux interrupteurs selon la table de correspondance donnée en annexe A. En utilisant un interrupteur on peut arrêter et relancer la détection d'erreurs à tout moment. Le résultat du calcul de taux d'erreurs binaires est indiqué sur les afficheurs 7 segments. De plus, deux signaux représentant respectivement le nombre d'erreurs et le nombre total de bits sont générés pour permettre le debug par simulation.

Cible matérielle

Le matériel utilisé est composé d’un PC et d’une carte électronique intégrant,

• le circuit intégré programmable FPGA (Field Programmable Gate Array) de type Artix-7 de Xilinx, sur une carte Nexys4 de Digilent
• les afficheurs 7 segments,
• les interrupteurs,
• les boutons poussoirs,
• un oscillateur à 100 MHz, pour fournir un signal d'horloge.

La figure suivante présente les différents éléments présents sur la carte. L’outil de conception de circuit, installé sur le PC (ou disponible à distance), est Vivado de Xilinx.

TP4 - La carte électronique composée, notamment, d’un FPGA, d’afficheurs 7 segments, de switchs et de boutons poussoirs

En supplément, on utilise une carte de conversion numérique-analogique (CNA) pour visualiser les signaux I et Q en sortie du canal à l'oscilloscope.

Circuit complet de MAQ16

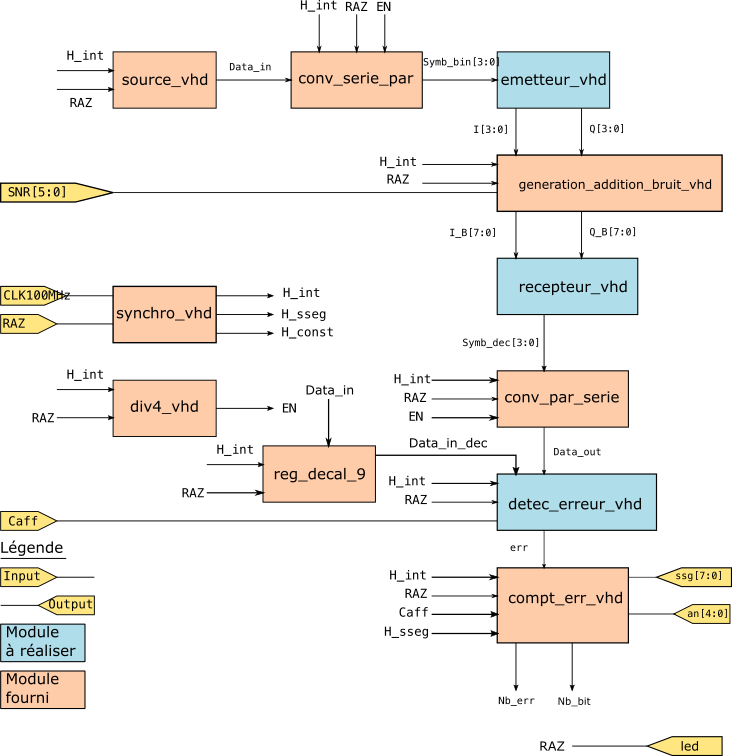
L'architecture du circuit complet est décrite figure suivante. Les blocs saumon sont fournis complet, ils n'ont pas à être modifiés. Les blocs bleu doivent être modifiés. Les ports d'entrée et sortie du circuit FPGA sont représentés en jaune. Toutes les flèches représentent des signaux internes au circuit FPGA.

TP4 - L'architecture du circuit complet

Principe de fonctionnement

Avant de lancer l'émulation de la transmission de données, il faut initialiser le circuit en positionnant RAZ à 1, puis en le remettant en 0. Le passage à 0 de RAZ lance la génération des données binaires par le module source. Après conversion série parallèle, les quatre bits du symbole de modulation MAQ16 entrent dans le module emetteur, qui les convertit en signaux I et Q. Les 6 interrupteurs SNR permettent de programmer l'écart-type du bruit ajouté par le module generation_addition_bruit. Les signaux I et Q sont alors bruités à l'aide de ce module. Les signaux bruités I_B et Q_B sont ensuite détectés par le module recepteur pour obtenir le symbole de modulation décidé. Après conversion parallèle série, la séquence de données binaires décidées est comparée à la séquence de données émises à l'aide du module detect_err. Le module compt_err compte les erreurs et fournit deux signaux de sortie qui correspondent au nombre d'erreurs et au nombre de bits total émis. Il fournit également deux signaux permettant d'afficher le résultat sur les afficheurs 7 segments. L'interrupteur Caff permet d'arrêter et de relancer la détection des erreurs.

Description des modules existants

Module synchro_vhd

Ce bloc fournit à partir de l'oscillateur CLK100MHz les différents signaux d'horloges du FPGA. Ces signaux sont nécessaires au fonctionnement du circuit global.

Entrées :

• CLK100MHz : signal en provenance de l’oscillateur de la carte Digilent.
• RAZ : signal de remise à zéro actionné par un bouton sur la carte Digilent.

Sortie :

• H_int : obtenue par division de 256 de CLK100MHz. C'est l'horloge débit des données.
• H_sseg : obtenue par division de fréquence de CLK100MHz. C'est l'horloge permettant l'affichage du résultat.
• H_const : obtenue par division de fréquence de CLK100MHz. Horloge non utilisée.

Module div4_vhd

Le bloc div4_vhd fournit un signal de contrôle EN utilisé par le bloc emetteur et le bloc recepteur. Ce module est un compteur modulo 4 dont un des 4 états est décodé : EN est à 1 pendant une période d'horloge et à 0 pendant les 3 autres. Ce signal est nécessaire au séquencement de la conversion série-parallèle et parallèle-série. Il doit être utilisé en ENABLE et non en signal d'horloge.

Entrée :

• H_int : signal en provenance du bloc synchro
• RAZ : signal de remise à zéro actionné par un bouton sur la carte FPGA.

Sortie :

• EN: signal de type Enable égal à 1 pendant une période de H_int sur 4.

Module source_vhd

La source fournit sur data_in une séquence pseudo-aléatoire de période \(2^{31}-1\), au rythme de H_int.

Entrées :

• H_int : signal en provenance du bloc synchro
• RAZ : signal d'initialisation au démarrage du circuit

Sortie

• Data_in : signal de données binaires pseudo-aléatoires en série,

Module compteur_err_vhd

Le bloc compt_err_vhd réalise le comptage des erreurs et gère l’affichage du taux d’erreurs binaires. Le comptage des erreurs est effectué sur des séquences de 1 Mbits. Le bloc gère ensuite l’affichage de ce nombre sur les 4 afficheurs 7 segments de la carte. La lecture se fait comme suit : le nombre d'erreurs est égal au nombre affiché par les 3 afficheurs de gauche multiplié par une puissance de 10 négative fournie par le 4ème afficheur. Exemple : sur la figure ci-dessous on lit le taux d'erreurs binaires \(606.10^{-4}\), c'est à dire \(6,06.10^{-2}\). Le signal nb_err comptabilise le nombre d'erreurs. Le signal nb_bits compte le nombre de bits depuis le début de la détection d'erreurs. Le démarrage de la détection d'erreurs est piloté par le signal Caff.

TP4 - Exemple d'affichage d'un taux d'erreurs binaires.

Entrée

• H_int : signal en provenance du bloc synchro
• RAZ : signal d'initialisation au démarrage du circuit
• Caff : signal d'arrêt et de relance de la détection d'erreurs
• H_sseg : obtenue par division de fréquence de CLK100MHz. C'est l'horloge permettant l'affichage du résultat.
• err : égal à 1 lorsqu’une erreur est détectée à la réception

Sorties

• s_aff[7:0] : permet l'affichage du taux d’erreurs binaires sur les afficheurs 7 segments
• an[4:0] : permet le choix de l'afficheur
• Nb_err : donne le nombre d'erreurs depuis le début du comptage
• Nb_bit : donne le nombre de bits passés dans le canal depuis le début du comptage

Module generation_addition_bruit_bhd

Ce bloc génère des échantillons de bruit blanc de distribution gaussienne et les ajoute aux symboles représentés par les voies I et Q. L'écart-type des échantillons de bruit est programmable à l’aide des interrupteurs présents sur la carte d’interface. La table de correspondance entre les interrupteurs SNR[5:0], l'écart-type et le rapport signal-à-bruit est donnée en Annexe A. Ce module suppose que les symboles non bruités fournis sur les voies I et Q sont codés en complément à 2. Les symboles bruités sont fournis sur 8 bits : 4 bits pour la partie entière et 4 bits pour la partie fractionnaire. La partie fractionnaire ne sert que pour la visualisation de la constellation.

Entrées :

• I[3:0] : signal représentant la voie en phase de la MAQ16 codée en complément à 2 sur 4 bits
• Q[3:0] : signal représentant la voie en quadrature de la MAQ16 codée en complément à 2 sur 4 bits

Sorties :

• I_B[7:0] : signal représentant la voie en phase bruitée en complément à 2 sur 8 bits
• Q_B[7:0] : signal représentant la voie en quadrature bruitée en complément à 2 sur 8 bits

Module conv_serie_par

Ce module réalise la conversion série parallèle du flux de données data_in vers une séquence de mots de 4 bits, constituant le 4-uplet du symbole de modulation MAQ16. Il utilise le signal EN, actif tous les 4 cycles d'horloge, généré par diviseur_freq.

Entrées :

• data_in : signal de données binaires en série,
• H_int : signal en provenance du module synchro,
• EN : signal de type Enable égal à 1 pendant une période de H_int sur 4.

Sortie :

• symb_bin[3:0] : séquence de mots de 4 bits, constituant le 4-uplet du symbole de modulation MAQ16.

Module conv_par_serie

Ce module réalise la conversion parallèle série des données décidées issues du module recepteur. Il utilise le signal EN, actif tous les 4 cycles d'horloge, généré par div4_vhd.

Entrées :

• symb_dec[3:0] : séquence de mots de 4 bits, constituant le 4-uplet du symbole de modulation MAQ16 après décision.
• H_int : signal en provenance du module \verb+synchro+,
• EN : signal de type Enable égal à 1 pendant une période de \verb+H_int+ sur 4.

Sortie :

• Data_out : signal de données binaires décidées en série

Cahier des charges des modules à concevoir

Les fonctionnalités des trois modules à concevoir sont décrites ci-dessous.

Module emetteur_vhd

Ce module combinatoire fournit les valeurs numériques de type réel signé en codage en complément à 2 sur 4 bits (pour chaque voie) des symboles modulés en MAQ16. La voie I donne la voie en phase et la voie Q donne la voie en quadrature. Le mapping qui répond aux deux contraintes suivantes est donné en Annexe A:

• Minimisation de la probabilité d’erreur
• Simplification de la détection des symboles au niveau du récepteur

Entrée :

• symb_bin[3:0] : séquence de mots de 4 bits, constituant le 4-uplet du symbole de modulation MAQ16.

Sorties :

• I[3:0] : séquence représentant la voie en phase de la MAQ16 codée en complément à 2 sur 4 bits (uniquement partie entière, car nombre entier signé)
• Q[3:0] : séquence représentant la voie en quadrature de la MAQ16 codée en complément à 2 sur 4 bits (uniquement partie entière, car nombre entier signé)

Module recepteur_vhd

Ce module réalise la détection des symboles bruités reçus. Pour cela, il reçoit les valeurs numériques codées en complément à 2 sur 8 bits de la voie en phase et la voie en quadrature représentant les symboles bruités. Seule la partie entière de ces valeurs numériques en complément à 2 sur 4 bits des symboles bruités sera utilisée pour réaliser la détection. Ce module fournit sur symb_dec[3:0] le 4-uplet du symbole de modulation décidé. Les règles de décision pour les voies I et Q sont données dans le TD de préparation en Annexe C

Entrées :

• I_B[7:0] : séquence représentant la voie en phase de la MAQ16 codée et bruitée en complément à 2 sur 8 bits, dont 4 bits de partie entière
• Q_B[7:0] : séquence représentant la voie en quadrature de la MAQ16 codée et bruitée en complément à 2 sur 8 bits, dont 4 bits de partie entière

Sortie :

• symb_dec[3:0] : séquence de mots de 4 bits, constituant le 4-uplet du symbole de modulation MAQ16 qui a été détecté.

Module detect_err_vhd

Ce module réalise la détection d’erreur. Pour cela, les signaux Data_in_dec et Data_out sont comparés. Si les signaux sont différents, la sortie err est égale à 1 et égale à 0 dans le cas contraire. Pour que la comparaison se fasse correctement, Data_in a été retardé d'un nombre de périodes égal à la latence de la chaîne de transmission. Ce retard est appliqué dans le module reg_decal_9. Remarque : le générateur de bruit n'introduit aucune latence.

Enfin, le signal Caff permet de relancer la détection d’erreurs à tout moment en interrompant la détection d’erreurs. Ce signal est directement relié à un bouton poussoir sur la carte. Le signal Caff peut être considéré comme un signal de validation du signal err.

Entrées :

• H_int : signal en provenance du bloc synchro
• RAZ : signal d'initialisation au démarrage du circuit
• Caff : signal d'arrêt et de relance de la détection d'erreurs
• Data_out : signal de données binaires décidées en série
• Data_in_dec : signal de données binaires pseudo-aléatoires en série, retardé d'un nombre de périodes égal à la latence de la chaîne de transmission.

Sortie :

• err : signal d'erreur égal à 0 si le bit détecté n'est pas erroné et 1 s'il y a une erreur.

Travaux pratiques en séance

Phase 1 - Description et simulation des modules combinatoires

Création du projet

Téléchargement de l'archive source

Une archive de fichiers sources vous est proposée sur https://moodle.imt-atlantique.fr/course/view.php?id=578#section-1. Cette archive, appelée SIT212_TP4_Source_files_vivado.tar.gz, vous permet de récupérer les fichiers sources VHDL de description et de simulation.

Une fois téléchargée, elle doit être décompressée dans un répertoire de travail que vous aurez judicieusement créé dans votre arborescence de fichiers, par exemple ~/SIT212/TP4/Fichiers_sources.

Warning

Ne mettez jamais d'espaces, d'accents ou des caractères spéciaux dans les noms de répertoires ou de fichiers

Ouverture de Vivado

Sous Linux, ouvrez un Terminal (Ctrl+Alt+T) et lancez la commande suivante

SETUP MEE_VIVADO_CLASSROOM && vivado&

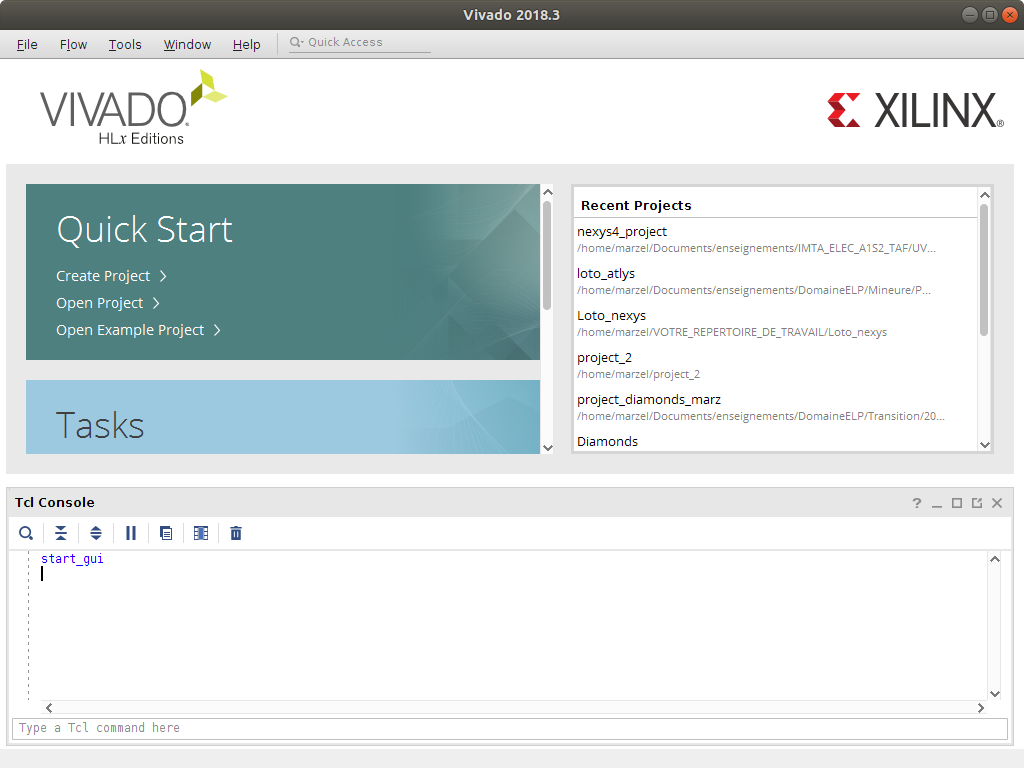
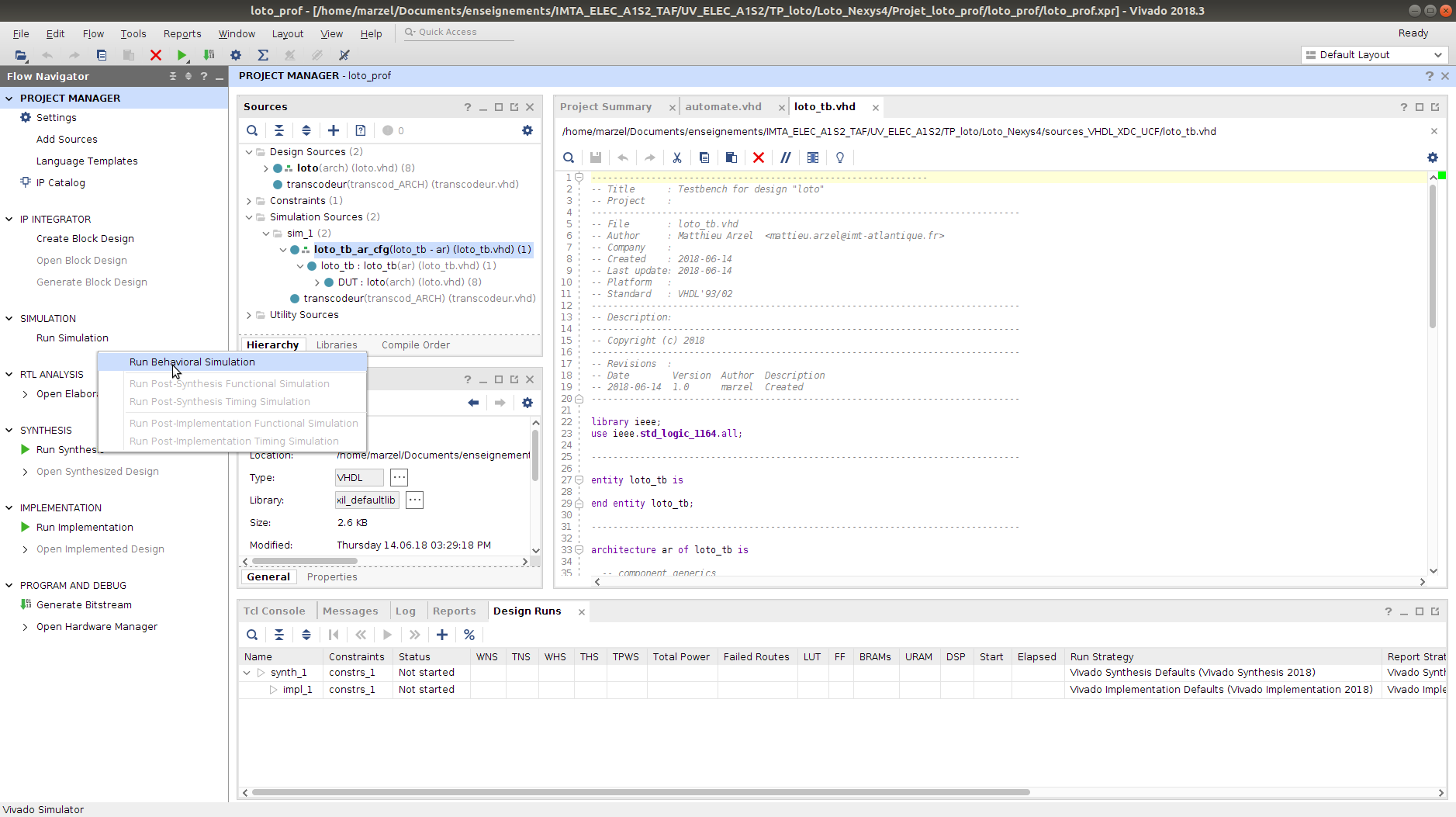
L'interface graphique de Vivado démarre alors (peut prendre un certain temps) et se présente telle qu'illustrée à la figure suivante.

Interface graphique de Vivado au démarrage.

Création d'un nouveau projet

Cliquez sur Create Project pour lancer l'assistant (wizard) de création de projet, puis cliquez sur Next sur la fenêtre qui apparaît alors.

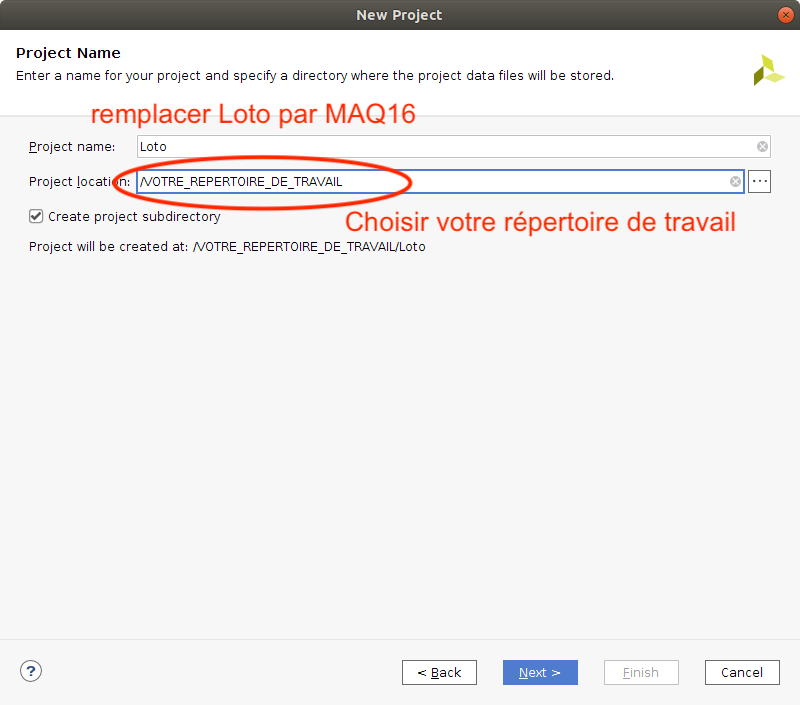
Dans la fenêtre suivante (voir ci-dessous), renseignez le nom de votre projet (MAQ16) et votre répertoire de travail ~/SIT212/TP4. Create project directory doit être coché.

Fenêtre de validation du nom et de la position du projet.

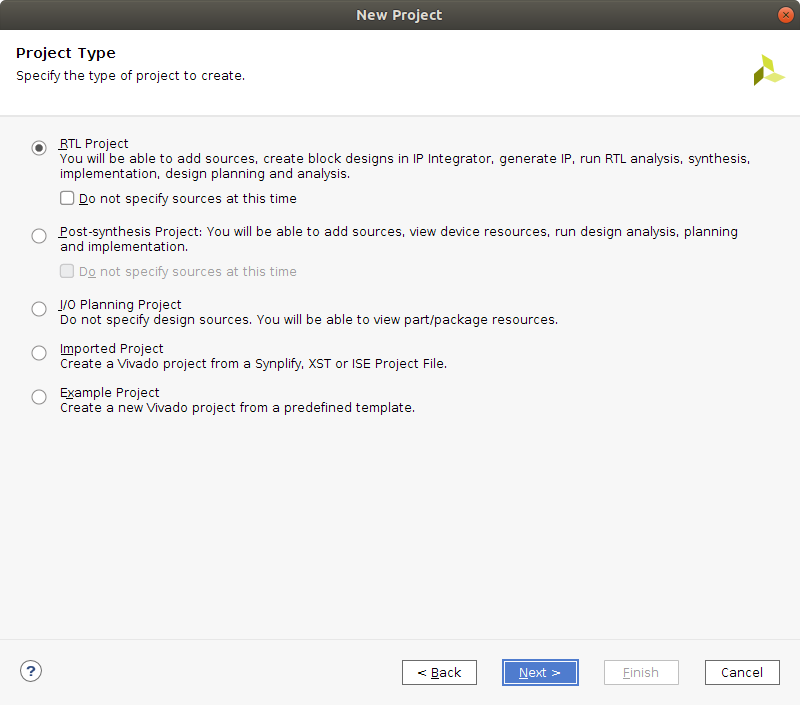
À la fenêtre suivante (voir ci-dessous), sélectionnez RTL Project pour créer un projet qui acceptera des sources VHDL.

Fenêtre de sélection du type du projet.

Ajout des fichiers sources et des contraintes

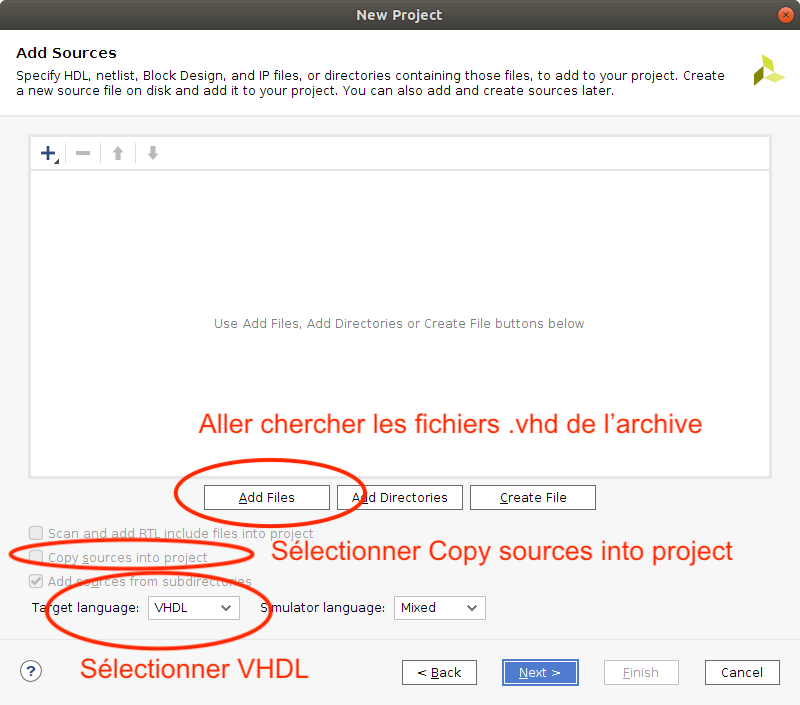
Validez encore avec Next pour passer à la fenêtre suivante qui vous demande vos fichiers sources (voir ci-dessous).

Fenêtre de sélection des fichiers sources pour le projet.

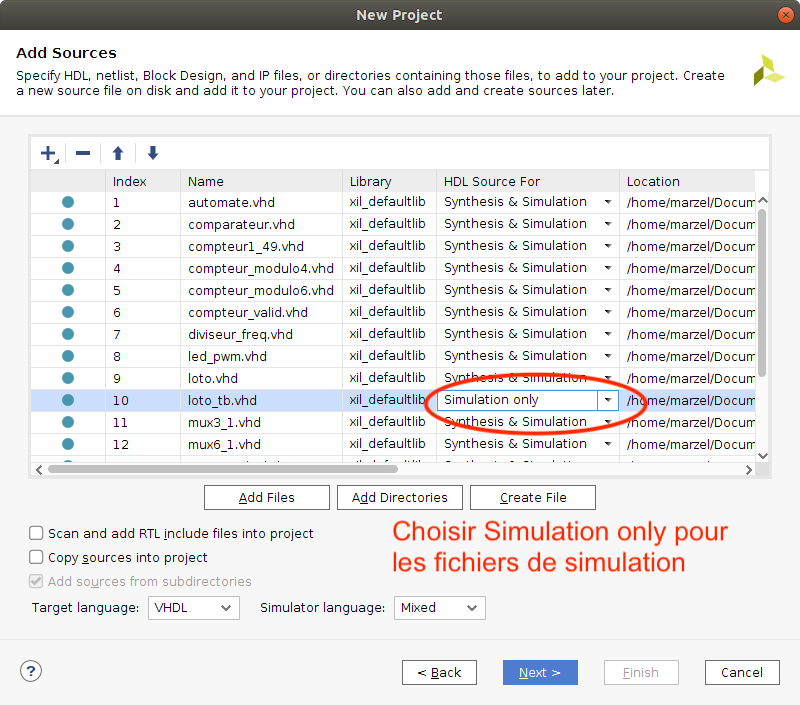
Sélectionnez alors tous les fichiers VHDL (en extension .vhd) de votre archive décompressée disponible dans les dossiers sources et sim. Puis modifiez le mode des fichiers de test, qui commencent par TB ou tb, en mode Simulation uniquement comme en figure suivante.

Modification du mode d'utilisation du fichier de testbench.

• Sélectionnez Copy sources into project.
• Sélectionnez Target langage VHDL.
• Cliquez sur Next pour valider.

Ne renseignez rien dans la fenêtre suivante (aucun module autre que décrit en VHDL ne sera utilisé) et continuez.

Sélection du FPGA utilisé

Apparaît alors la fenêtre Add Constraints. Sélectionnez le fichier MAQ16_Top.xdc dans le répertoire constrs.

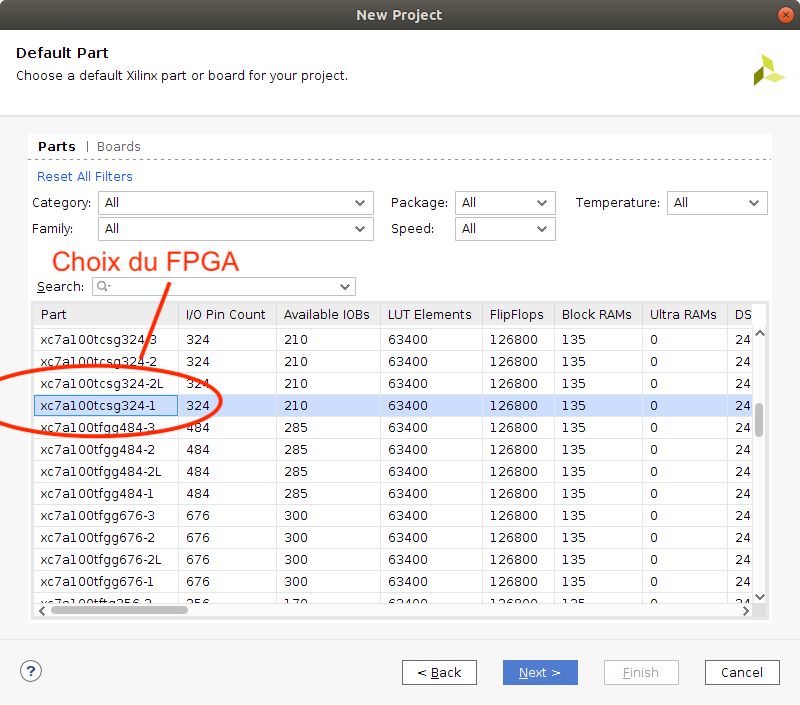
Après validation apparaît la fenêtre de sélection de la cible matérielle FPGA que vous renseignez tel qu'indiqué sur la figure suivante. Cela vous permet de choisir le FPGA de la carte (xc7a100tcsg324-1 de son petit nom).

Fenêtre de sélection du FPGA cible.

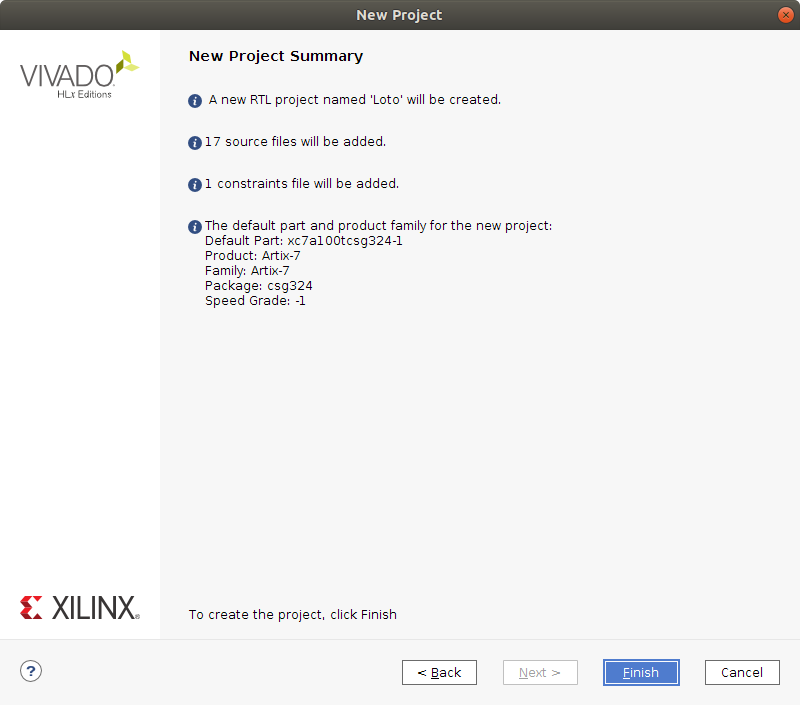
La fenêtre suivante résume votre projet et doit être identique à celle présentée en figure suivante.

Fenêtre de validation pour la création du projet Vivado.

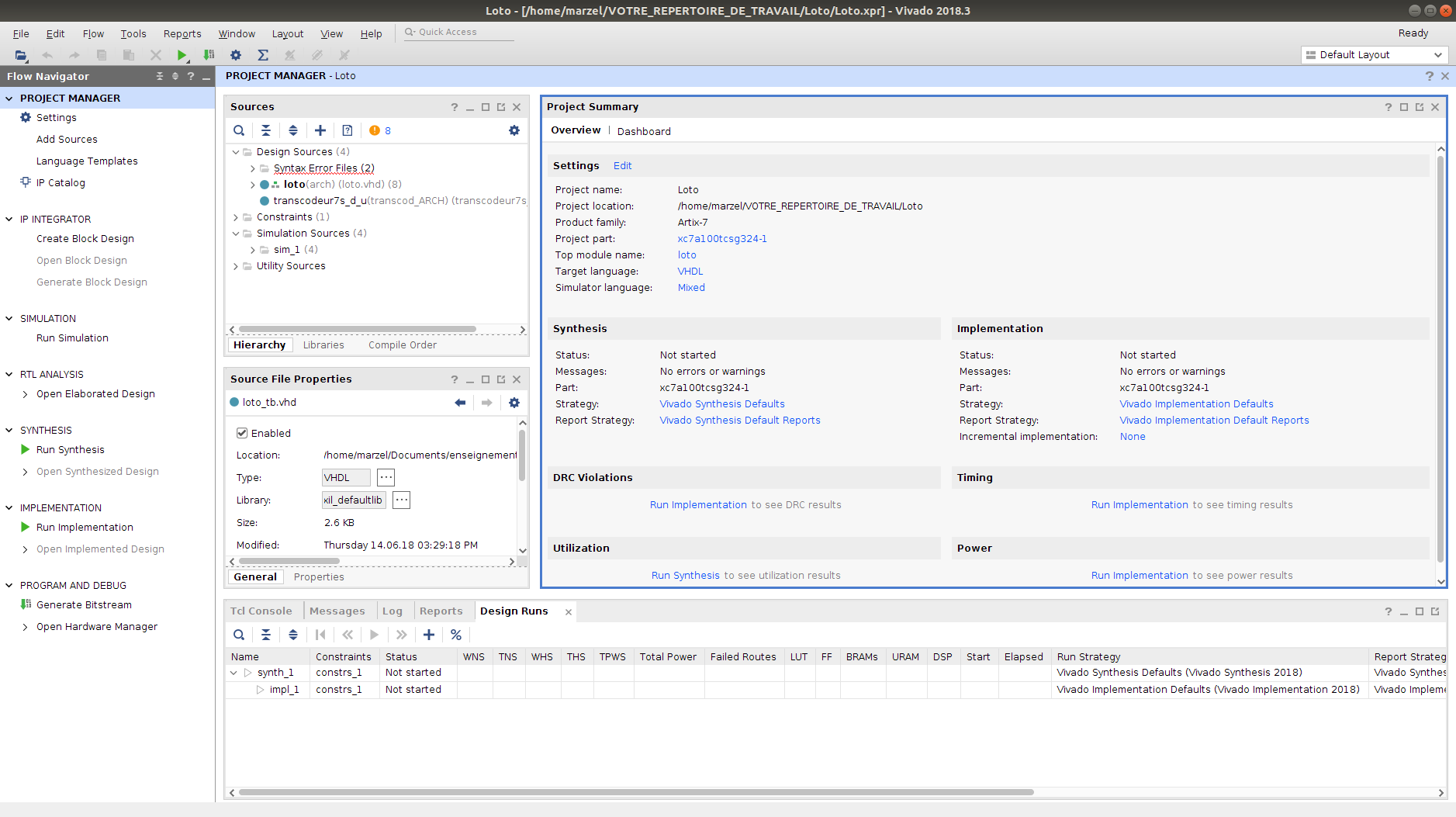
Le projet est ensuite créé et l'interface projet de Vivado se lance comme en figure suivante.

Interface projet Vivado.

Description partielle du module combinatoire emetteur_vhd en VHDL

• Dans la fenêtre PROJECT MANAGER / Sources développez l'onglet Design Sources. Puis MAQ16_Top.
• Ouvrez le fichier emetteur_vhd.vhd, dont certaines parties ont été remplacées par _BLANK_.
• À partir de votre travail préparatoire sous la forme d'une table de vérité, et de la description VHDL de la structure case décrite dans l'Aide-mémoire VHDL,
• remplacez les sections _BLANK_ par du code approprié.

Question 1

• À quoi servent les signaux intermédiaires I_int et Q_int ? En quoi est-ce lié au choix du mapping MAQ16 ?
• Consultez la section Examples-of-synthesizable-vhdl de l'Aide-mémoire VHDL pour comprendre la notion de process et de liste de sensibilité (sensitivity list) des processus asynchrones (c.a.d. combinatoires). Dans le cadre de ce module emetteur_vhd, quels sont les signaux à renseigner dans la liste de sensibilité de chacun des 2 processus ? Pourquoi ?
• Expliquez la notion de processus concurrents.

Simulation VHDL du module emetteur_vhd

Pour valider ensuite votre module emetteur_vhd, vous le simulez avec l'outil XSIM de Vivado. Pour cela un fichier de test vous est proposé: TB_emetteur.vhd, aussi disponible par la fenêtre Sources, onglet Simulation Sources / sim_1. Sélectionnez ce module.

Puis, cliquez sur le bouton droit de la souris pour faire apparaître le menu contextuel et cliquez sur Set as Top. Ainsi, ce module pourra être simulé en cliquant dans le panneau de gauche Flow Navigator / Project Manager sous l'onglet Simulation Run Simulation Run Behavioural Simulation.

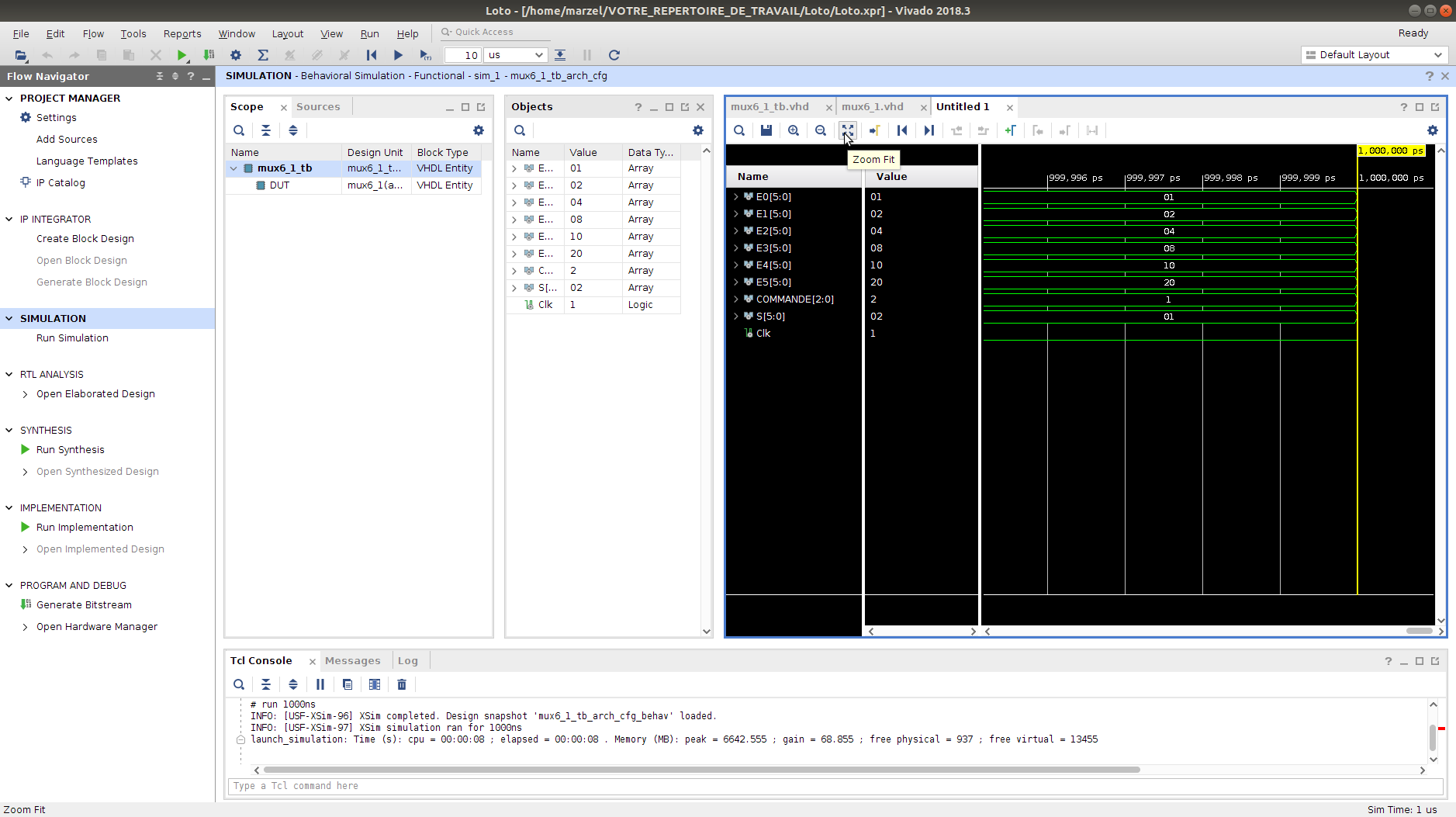
La fenêtre illustrée en figure suivante apparaît alors.

Interface de simulation de Vivado.

Choix du Zoom

Cliquez sur Zoom Fit puis ajustez le zoom jusqu'à pouvoir analyser le chronogramme de la simulation et ainsi vérifier que votre description VHDL fournit le comportement attendu.

Format de représentation des nombres dans la simulation

Dans le chronogramme résultat de la simulation, chaque signal binaire affiché peut être représenté sous différents formats : binaire naturel, réel signé, réel non signé, hexadécimal, etc. Cette représentation (ou radix d'affichage) est au choix du concepteur et peut être choisi afin de faciliter la lecture des résultats de simulation. Par exemple, pour modifier le radix d'affichage d'un signal en décimal non signé cliquez sur le nom d'un signal, avec le bouton DROIT de la souris, puis sur radix > unsigned decimal.

Tip

Choisissez astucieusement les représentations de vos signaux d'entrée et sortie pour vous faciliter la tâche d'analyse de la simulation.

Question 2

Toutes les réponses aux questions doivent être illustrées par des copies écrans des simulations.

• Justifiez vos choix de format de représentation des nombres pour les signaux d'entrée et de sortie.
• Observez le résultat de simulation et analysez-le. Observez également le fichier de testbench. Pourquoi cette simulation ne permet-elle pas de valider le module de manière complète et exhaustive ?
• En lien avec la question précédente, modifiez le ficher de testbench, et relancez la simulation.
• Analysez le résultat de cette 2ieme simulation et justifiez la validation du module.

Description partielle du module combinatoire recepteur_vhd en VHDL

• Quittez la simulation en fermant la sous-fenêtre de simulation.
• Dans la fenêtre PROJECT MANAGER / Sources développez l'onglet Design Sources.
• Ouvrez le fichier recepteur_vhd.vhd, dont certaines parties ont été remplacées par _BLANK_.

À partir de votre travail préparatoire sous la forme de fonctions logiques, et de la description VHDL des fonctions logiques combinatoires décrites dans l'Aide mémoire VHDL, remplacez les sections _BLANK_ par du code approprié.

Question 3

• Quels sont les bits de I et Q qui correspondent à la partie entière des nombres qu'ils représentent ?
• Expliquez pourquoi seule la partie entière est utilisée dans l'obtention du symbole décidé b_int (ou Symb_dec) et le rôle de la troncature par défaut dans la règle de décision du bit Symb_dec[2]} et Symb_dec[0].
• Expliquez pourquoi cela réduit la complexité du circuit qui sera généré.

Simulation VHDL du module recepteur_vhd

Pour valider de nouveau votre description VHDL, vous devez simuler le module avec le fichier de test proposé: TB_recepteur.vhd. Pour cela, cliquez sur ce fichier puis clic bouton droit de la souris et choisissez Set As Top. Puis effectuez la simulation comme précédemment.

Dans le chronogramme, les signaux I et Q sont représentés sur 8 bits. Pour faciliter la lecture, nous souhaitons récupérer uniquement les 4 bits de poids forts. Pour cela, dans la fenêtre Objects, développez I_B[7:0] et Q_B[7:0]. Glissez-déposez les signaux correspondants aux bits de poids forts dans la fenêtre qui liste les signaux du chronogramme (sous Name). Toujours en gardant les 4 signaux correspondant aux bits de poids fort sélectionnés, cliquez DROIT et choisissez New virtual bus. Donnez lui un nom explicite. }

Pour faciliter la lecture, vous pouvez changer le radix d'affichage. En particulier, pour les signaux d'entrée, vous pouvez utiliser Real settings puis choisir fixed point, signed, binary point 4. Pour les bits de poids fort (la partie entière après troncature), choisissez signed decimal.

Question 4

Toutes les réponses aux questions doivent être illustrées par des copies écrans.

• Observez et analysez le résultat de la simulation. À quoi comparez-vous le résultat de votre simulation ? En quoi cette simulation valide-t-elle fonctionnellement le module ?
• À partir de la simulation, (faites des copies écran), donnez des exemples de troncatures pour des signaux reçus I_B et Q_B positifs et négatifs. Expliquez les décisions prises au niveau binaire Symb_dec[3:0] au regard des règles de décision de la MAQ16.

Description partielle du module combinatoire detect_err en VHDL

• Quittez la simulation en fermant la sous-fenêtre de simulation.
• Dans la fenêtre PROJECT MANAGER / Sources développez l'onglet Design Sources.
• Ouvrez le fichier detect_err_vhd.vhd, dont certaines parties ont été remplacées par _BLANK_.

À partir de votre travail préparatoire sous la forme de fonctions logiques, et de la description VHDL des fonctions logiques combinatoires décrites dans l'Aide mémoire VHDL, remplacez les sections _BLANK_ par du code approprié.

Simulation VHDL du module detect_err

Pour valider de nouveau votre description VHDL, vous devez simuler le module avec le fichier de test proposé: TB_detect_err.vhd. N'oubliez pas Set As Top.

Phase 2 - Simulation et test du circuit complet

Pour valider par simulation l'intégration des 3 modules, vous devez simuler l'intégralité du circuit de MAQ16.

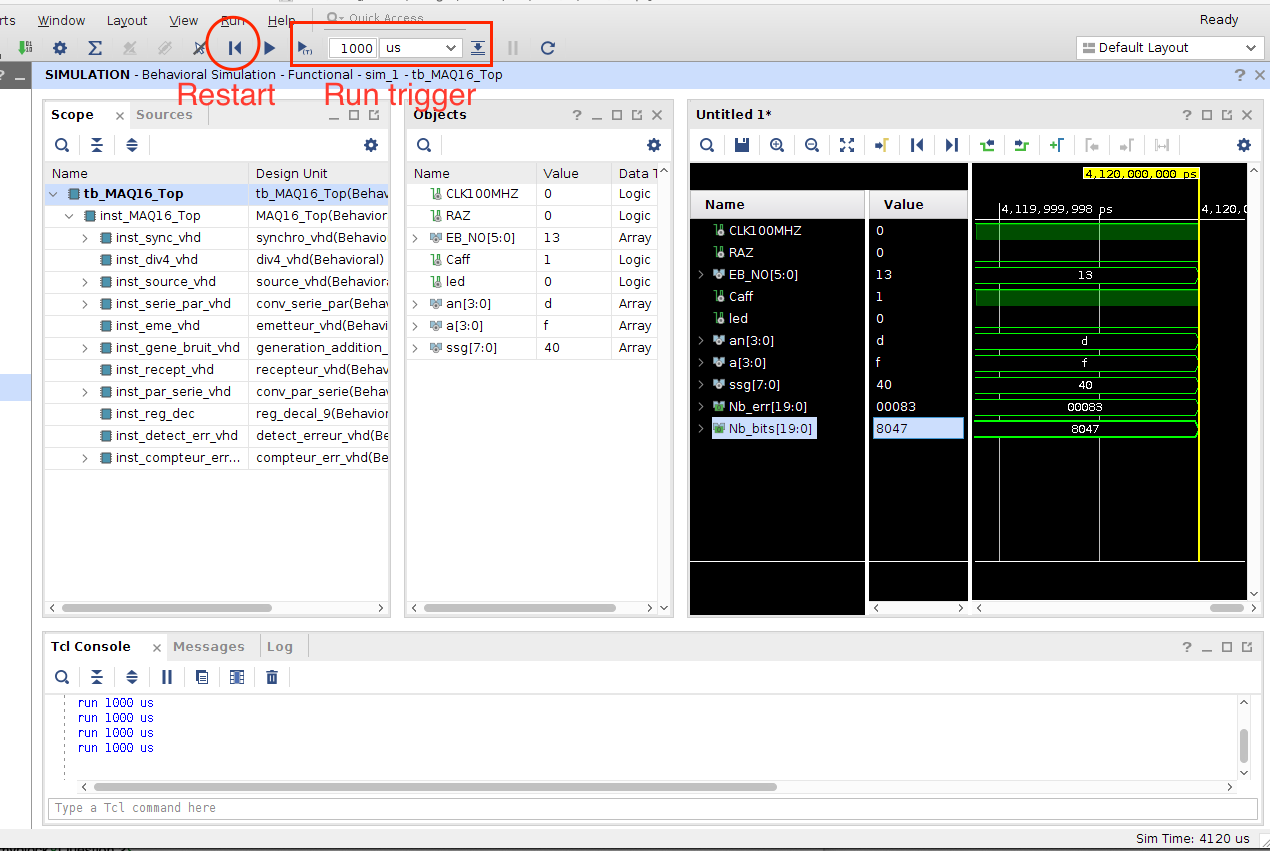
Passez donc le module tb_MAQ16_Top.vhd en TOP et simulez le circuit comme illustré en figure suivante.

Lancement de la simulation complète du circuit MAQ16.

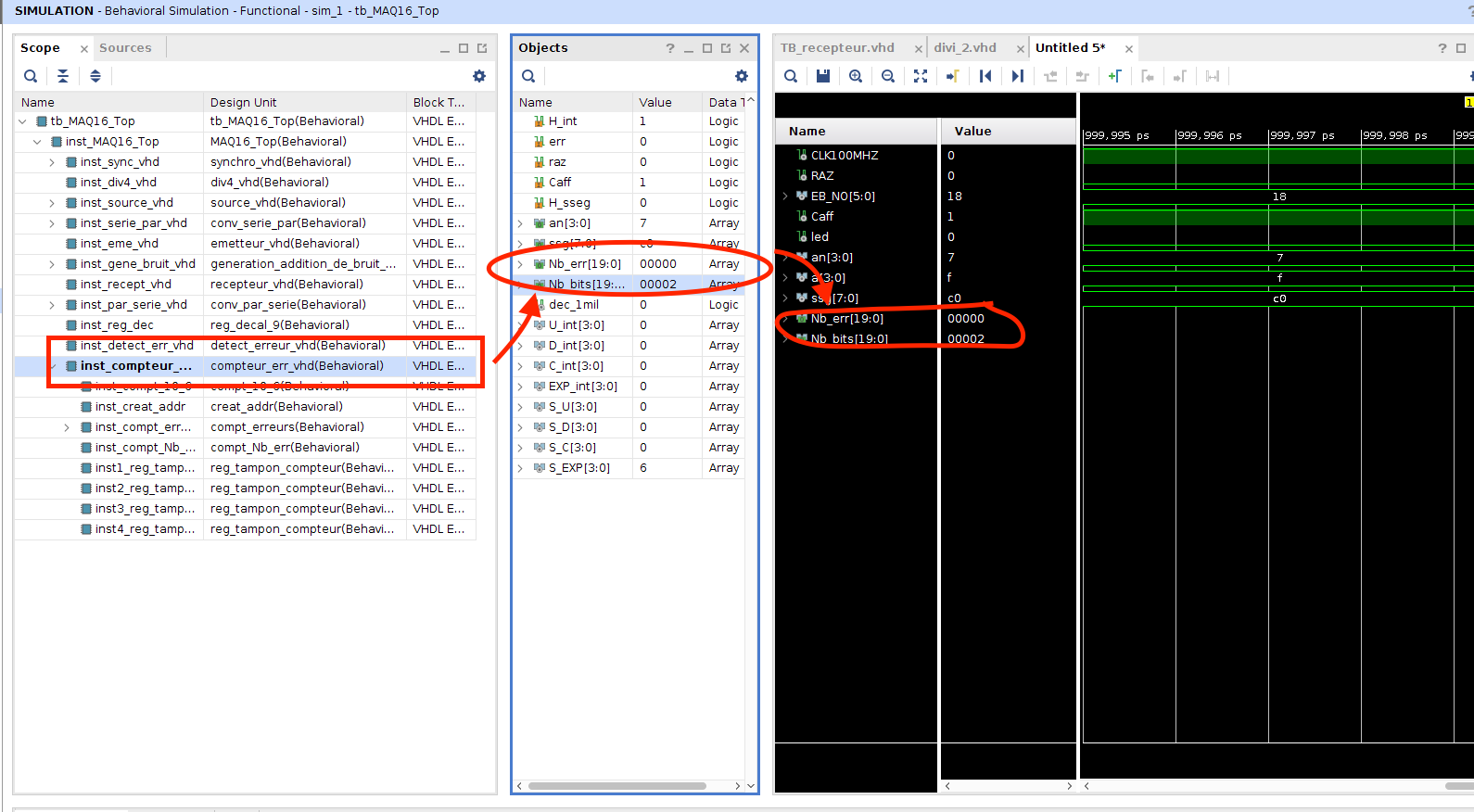
Cependant, les signaux Nb_err et Nb_bits, qui ne font pas partie des ports d'entrée/sortie du circuit, n'apparaissent pas. Pour les ajouter à la simulation, dans la fenêtre SIMULATION / Scope développez inst_MAQ16_Top puis cliquez sur inst_compteur_erreur_vhd. Dans la fenêtre SIMULATION / Objects glissez-déposez les signaux Nb_err et Nb_bits dans la fenêtre de simulation pour les faire apparaître dans la liste de signaux à simuler :

Ajout des signaux `Nb_err` et `Nb_bits` à la simulation.

Puis cliquez sur Restart. Enfin, cliquez sur Run trigger :

Relancer la simulation après ajout des signaux.

Question 5

Toutes les réponses aux questions doivent être illustrées par des copies écrans des simulations.

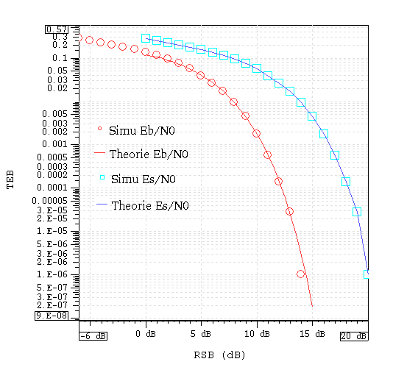
La correspondance entre le signal SNR[5:0] et \(SNR = E_s/N_0\) en dB est donnée dans le tableau des SNR. Les courbes théorique et simulée sous MATLAB de la probabilité d'erreur de la MAQ16 sont données figure TEB MAQ 16.

• Expliquez pourquoi aucune erreur n'est détectée (Nb_err est égal à 0) lors du 1er lancement de la simulation.
• Que se passe-t-il lorsqu'on relance la simulation en cliquant plusieurs fois sur Run trigger ?
• Quel est le taux d'erreurs obtenu ? Pour quelle valeur du signal SNR[5:0] et donc quelle valeur de SNR en dB (cf. tableau des SNR) ? Est-ce que cela correspond à la courbe théorique donnée à la figure TEB MAQ 16 ? (\(SNR = E_s/N_0\))
• Vérifiez un autre point de la courbe en modifiant le signal SNR[5:0] dans le fichier de testbench. Vous placez les points directement sur la figure (faîtes une copie écran).
• Dans le fichier de simulation tb_MAQ16_Top.vhd, modifiez le signal SNR[5:0] pour qu'il représente une valeur de 24,02 dB, puis relancez la simulation pour vérifier le nouveau taux d'erreurs. Qu'observez-vous ? Pourquoi ?

Phase 3 - Elaboration, synthèse, placement, routage et implantation du circuit sur FPGA

Maintenant que le circuit est validé en simulation, vous allez passer au test sur carte. Si vous passez les phases de compilation matérielle que sont l'élaboration, la synthèse, le placement et le routage avec succès ! Passez le module MAQ16_top.vhd en TOP. N'oubliez pas cette étape!!!

Ensuite :

• revenez au panneau de gauche Flow Navigator / Project Manager
• cliquez sous Program and Debug sur la commande generate bitstream et acceptez ensuite les paramètres par défaut.

L'outil vous produit alors un fichier de configuration du FPGA qui spécifie comment le FPGA sera utilisé pour fournir le circuit conçu en VHDL et contraint par le fichier qui spécifie les entrées/sorties.

Test du circuit sur FPGA

Une fois le bitstream généré, allez récupérer le fichier MAQ16_top.bit dans le dossier MAQ-16.runs/impl_1 puis déposez-le sur Moodle https://moodle.imt-atlantique.fr/mod/assign/view.php?id=55870.

Testez sur la carte disponible au PC prof !

L'affichage du taux d'erreurs binaires sur la carte est donné pour des paquets de \(10^6\) bits.

Question 6

Pour illustrer vos réponses, prenez une photo du circuit en cours de fonctionnement.

• Qu'observez-vous sur la carte ? Comment vérifier que le fonctionnement observé est conforme au cahier des charges ?

• Quel est la taille des paquets de bits transmis ? Jusqu'à quel rapport signal-à-bruit observez-vous un taux d'erreurs binaires non nul ? Que faudrait-il faire pour pouvoir observer un taux d'erreurs binaires plus faible ? Est-ce possible en simulation ? Expliquez pourquoi.

• Si vous avez eu besoin de débugger et de produire une nouvelle version du code, expliquez pourquoi.

Évaluation

L’évaluation est réalisée à partir d’un QCM sur le travail préparatoire et d’un rapport de compte-rendu de TP sur la plateforme LabnBook. https://moodle.imt-atlantique.fr/mod/labnbook/view.php?id=55194 ainsi que les consignes sont données sous Moodle.

Annexe A : La modulation numérique MAQ16

Dans le cadre d'une transmission numérique, la modulation d'amplitude en quadrature à 16 symboles (MAQ-16) est une modulation numérique à forte efficacité spectrale permettant de transmettre 4 bits/s/Hz, soit 4 bits par symbole. Le signal de sortie \(s(t)\) est donné par :

\[ s(t) = A(t). cos(2\pi f_c t) \]

avec \(A(t)=I(t)+jQ(t)\), \(I(t)\) la partie réelle, \(Q(t)\), la partie imaginaire du symbole tranmis \(A(t)\). Dans le cas de la modulation MAQ-16, \(A(t)\) peut prendre 16 valeurs différentes, appelées aussi états. \(I(t)\) et \(Q(t)\) sont alors des signaux discrets, c'est-à-dire que \(I(t)\) et \(Q(t)\) prennent des valeurs discrètes à chaque instant \(t\).

On peut représenter tous les états (ou symboles) \(A(t)\) par un diagramme de constellation présenté à la figure suivante. Celui représente la position des 16 symboles dans le plan complexe. Enfin, à chacun de ces 16 symboles est associé un mot binaire de 4 bits, puisqu'il y a \(16=2^4\) états possibles. Dans l'architecture du système, le mot binaire est représenté par symb_bin[3:0], avec symb_bin[3], le bit de poids fort.

Mapping MAQ16

Le choix de cette association entre état et mot binaire, appelé conversion binaire-Maire (ou mapping), n'est pas fait au hasard. Le mapping va vérifier 2 contraintes :

• minimisation de la probabilité d'erreur pour une transmission sur un canal à bruit blanc additif gaussien,
• réduction de la complexité du détecteur.

Tout d'abord, le mapping doit minimiser la probabilité d'erreur pour une transmission sur un canal à bruit blanc additif gaussien. Pour cela, le mapping doit suivre le codage de Gray. Vous pouvez observer qu'un 1 seul bit change entre 2 symboles adjacents.

Exemple : choisissons le symbole positionné en (-1;+1) correspondant à 0111. Les 4 symboles les plus proches sont 0110, 0011, 1111, 0101.

Ainsi, si le bruit est suffisamment fort pour déplacer le symbole en (-1;+1) vers le symbole en (+1;+1), 1 seul bit sera en erreur (dans cet exemple, le bit de poids fort).

De plus, afin de réduire la complexité du détecteur, nous choisissons que les bits symb_bin[3:2] (resp. symb_bin[1:0] codent la voie I (resp. Q). Ainsi, les 2 voies peuvent être codées et décodées indépendamment et donc en parallèle. Nous obtenons ainsi le mapping donné à la figure Mapping MAQ16.

Enfin, dans l'architecture du système \(I(t) \in \{-3;-1; 1;+3\}\), nombre entier et signé pour la constellation choisie , est représenté I[3:0], nombre binaire représenté en complément à 2, avec I[3], le bit de signe. De même, \(Q(t)\) est représenté par Q[3:0].

• Exemple 1 : si symb_bin[3:0] = 1011, alors I[3:0] = 0011 (+3) et Q[3:0] = 0001 (+1).
• Exemple 2 : si symb_bin[3:0] = 0100, alors I[3:0] = 1111 (-1) et Q[3:0] = 1001 (-3).

Si besoin, vous pouvez réviser la représentation en complément à 2 des nombres binaires, rappelée en Annexe E.

Au niveau de la réception, il faut définir des règles de décision en fonction des informations reçues sur les 2 voies en quadrature. Dans l'architecture du système, I_B et Q_B sont les signaux bruités reçus sur les voies I et Q. Ils représentent des signaux réels mais, dans notre système numérique, ils sont codés sur 8 bits, dont 4 pour la partie entière et 4 pour la partie décimale.

Du fait des choix réalisés sur la constellation et le mapping, seules les parties entières de I_B et Q_B sont utilisées pour décider du symbole reçu. En effet, les deux règles de décision pour la voie I sont les suivantes :

• Si le signe de I_B est positif, i.e. I_B[7]=0, alors symb_dec[3] est égal à 1, 0 sinon,
• Si \(-2 <\) I_B \(< +2\), alors symb_dec[2] est égal à 1, 0 sinon.

Les règles pour la voie Q sont identiques et permettent d'obtenir symb_dec[1] et symb_dec[0].

Annexe B : Performances théoriques de la MAQ16

La figure TEB MAQ 16 présente les performances théoriques (marqueurs) selon l'équation MAQ 16, avec \(M\) le nombre d'états de la modulation, soit 16 ici, et simulées (par MATLAB, lignes) de la modulation MAQ16 en termes de taux d'erreurs binaires versus rapport signal-à-bruit (énergie par symbole sur énergie du bruit \(E_s/N_0\)) dans le cas d'un canal à bruit blanc additif gaussien.

Les performance théoriques sont données par cette équation (voir cours de MTS 210 pour la démonstration):

\[ P_b = \frac{2}{\log_2(M)} \left(1-\frac{1}{\sqrt{M} } \right) \mathrm{erfc} \left( \frac{1}{\sqrt{2}} \sqrt{\frac{3}{M-1} E_s/N_0} \right) \]

Performances théoriques et simulées de la MAQ16 en termes de taux d'erreurs binaires versus rapport signal-à-bruit. RSB = SNR = ES/N0

Annexe C : TD de préparation, Bureau d'étude

L'objectif de ce bureau d'étude est de réaliser la conception des modules \verb+emetteur_vhd+, \verb+recepteur_vhd+, et \verb+detect_err_vhd+ :

• Concevoir le module emetteur_vhd sous la forme d'une table de vérité (cf. Emetteur).
• Concevoir le module recepteur_vhd sous la forme de fonctions logiques combinatoires (cf. Recepteur).
• Concevoir le module detect_err_vhd sous la forme d'une fonction logique combinatoire (cf. Detecteur).

Le nommage des entrées/sorties tel que défini à la section cahier des charge et sur la figure du Circuit complet sera respecté.

emetteur_vhd

• À l'aide des éléments du cahier des charges, identifier l'entrée et les sorties de ce module, ainsi que la taille du mot binaire.
• Justifier l'utilisation du mapping (conversion binaire à symbole) donné à la figure Mapping MAQ16.
• À partir du mapping choisi, donner la table de vérité du module.

recepteur_vhd

• À l'aide des éléments du cahier des charges, identifier l'entrée et les sorties de ce module, ainsi que la taille du mot binaire.
• Sur la figure Mapping MAQ16, identifier les seuils de décision permettant d'obtenir les symboles binaires décidés symb_dec[3:0], sachant que la voie I porte l'information de symb_bin[3:2] et Q celle de symb_bin[1:0], selon le principe d'indépendance des 2 axes.
• Justifier pourquoi seule les parties entières de I_B et Q_B doivent être utilisées.
• Enoncer la règle de décision permettant d'obtenir symb_dec[3] et symb_dec[1].
• Avant d'énoncer la règle de décision pour symb_dec[2] et symb_dec[0], quelques exercices de conversion de nombres décimaux en base 10 vers la base 2 selon le codage complément à 2 (CA2) sur 8 bits, dont 4 bits de partie entière : \(+1,5\) \(+2\) \(+2,5\) \(-1,5\) \(-2\) \(-2,5\). L'annexe E rappelle les notions vues en ELP111 sur ce sujet.
• À partir des observations réalisées à la question précédente, établir les règles de décision qui permettent d'obtenir symb_dec[2] et symb_dec[0] à partir de la partie entière de I_B et Q_B.
• À partir des 2 règles de décision obtenues, donner la table de vérité du module puis les fonctions logiques combinatoires simplifiées correspondantes.

detect_err_vhd

• À l'aide des éléments du cahier des charges, identifier les entrées et la sortie de ce module.
• Donner la table de vérité du module puis la fonction logique combinatoire simplifiée correspondante.

Annexe D : tableau de correspondance pour le choix du RSB

Le tableau des SNR présente la correspondance entre les interrupteurs (SNR[5:0]), l'écart-type du bruit \(\sigma_b\) et le rapport signal-à-bruit \(SNR =E_s/N_0=10\textrm{log}_{10} \frac{1}{2\sigma^2_b}\) (dB).

SNR[5:0]	\(\sigma_b\)	\(SNR\) (dB)	SNR[5:0]	\(\sigma_b\)	\(SNR\) (dB)
000001"	110111	8,3	100001"	10110	16,26
000010"	110101	8,62	100010"	10101	16,67
000011"	110100	8,79	100011"	10100	17,09
000100"	110010	9,13	100100"	10100	17,09
000101"	110001	9,31	100101"	10011	17,54
000110"	101111	9,67	100110"	10011	17,54
000111"	101110	9,86	100111"	10010	18
001000"	101101	10,05	101000"	10010	18
001001"	101011	10,44	101001"	10001	18,5
001010"	101010	10,65	101010"	10001	18,5
001011"	101001	10,86	101011"	10000	19,03
001100"	101000	11,07	101100"	10000	19,03
001101"	100111	11,29	101101"	1111	19,59
001110"	100110	11,52	101110"	1111	19,59
001111"	100100	11,99	101111"	1110	20,19
010000"	100011	12,23	110000"	1110	20,19
010001"	100010	12,48	110001"	1101	20,83
010010"	100001	12,74	110010"	1101	20,83
010011"	100000	13,01	110011"	1101	20,83
010100"	100000	13,01	110100"	1100	21,53
010101"	11111	13,29	110101"	1100	21,53
010110"	11110	13,57	110110"	1100	21,53
010111"	11101	13,86	110111"	1011	22,28
011000"	11100	14,17	111000"	1011	22,28
011001"	11011	14,48	111001"	1011	22,28
011010"	11010	14,81	111010"	1010	23,11
011011"	11010	14,81	111011"	1010	23,11
011100"	11001	15,15	111100"	1010	23,11
011101"	11000	15,51	111101"	1001	24,02
011110"	11000	15,51	111110"	1001	24,02
011111"	10111	15,88	111111"	1001	24,02
100000"	10110	16,26	AUTRES	111000	8,15

Annexe E : Rappels sur le codage des nombres entiers et réels signés en complément à 2

Codage en complément à 2 pour les nombres signés

Extrait de Fiche séance PC3

Il est visible sur les deux exemples précédents que la conversion peut ne pas se terminer et que l’on obtient, en s’arrêtant à un nombre fini de positions une approximation de la représentation du nombre.

Maintien de la résolution pour les nombres réels positifs

Soit (\(a_na_{n-1}\cdots a_0,a_{-1}\cdots a_{-m})_{(10)}\) et \((a_pa_{p-1}\cdots a_0,a_{-1}\cdots a_{-k} )_{(b)}\) les numérotations de position d’un même nombre N exprimé respectivement en base \(10\) et en base \(b\). La résolution d’une base \(b\) est définie comme étant la différence entre 2 nombres consécutifs dans cette base.

Elle est donc égale à \(b^{-k}\).

Ainsi, la résolution est conservée lors du passage de la base \(10\) à la base \(b\) si et seulement si la résolution du nombre transformé en base \(b\) est inférieur ou égal à la résolution de ce nombre en base \(10\). \(b^{-k}\) \leq 10^{-m}, c’est-à-dire si \(k log b\) \geq m log 10, soit

\[ k \geq m\frac{log 10}{log b} \]

• Exemple 1 : pour conserver la résolution lors du passage de \(0,925_{(10)}\) en base \(2\), il faut garder \(k \geq 3\frac{log 10}{log 2} \approx 9,97\) soit 10 bits après la virgule
• Exemple 2 : pour conserver la résolution lors du passage de \(0,45_{(10)}\) en base \(8\), il faut garder \(k \geq 2\frac{log 10}{log 8} \approx 2,2\) soit 3 bits après la virgule log10 garder

Représentation binaire des nombres signés (complément à 2)

Les systèmes numériques doivent être capables de traiter des nombres positifs et négatifs. L’utilisation d’une représentation signée suppose l’utilisation d’un format (nombre de bits) fixé au préalable.

Représentation en complément à 2

Le complément à 2 est le mode de représentation le plus utilisé en arithmétique binaire et donc dans les ordinateurs pour coder les nombres entiers.

Dans cette représentation, les nombres positifs se représentent par leur valeur binaire naturelle. Par exemple +6 est représenté par 0000 0110 sur un format de 8 bits.

La représentation des nombres négatifs s’obtient comme suit :

1. On part de la représentation binaire naturelle de l’opposé arithmétique du nombre à coder (nombre positif)
2. On calcule son complément à 1 (CA1) ou complément restreint. Celui-ci est obtenu en inversant tous ses bits
3. On en déduit son complément à 2 (CA2) ou complément vrai en ajoutant 1 au niveau du LSB, c'est-à-dire en réalisant l’addition binaire du complément à 1 et de 1.

Exemple : représentation de \(-5\) en CA2 sur un format de 8 bits

1. Représentation binaire naturelle de \(+5\) : \(5\) = 0000 0101
2. CA1 de \(+5\) : \(\overline{5}\) = 1111 1010
3. CA2 de \(+5\) : \(-5\) = 1111 1011

On identifie le CA2 d’un nombre à son opposé arithmétique, car \(A+(-A)=2^n=0\mod 2^n\) , si \(n\) est le format de représentation du nombre \(A\). En effet, soit \(A = a_{n-1}\cdots a_1a_0\) , alors \(\overline{A}=\overline{a_{n-1}}\cdots \bar{a_1}\bar{a_0}\), et donc \(A + \bar{A} = 11\cdots 11\) , soit \(A+\bar{A}=2^{n-1}\), et \(-A=\bar{A}+1\).

La représentation en complément à 2 présente les caractéristiques suivantes :

• Le principe d’obtention de l’opposé d’un nombre négatif est le même que celui permettant d’obtenir l’opposé d’un nombre positif
• Le nombre 0 a une représentation unique
• Un format sur n bits permet de coder en CA2 les nombres N vérifiant

\[ -2^{n-1} \leq N \leq +2^{n-1}-1 \]

Par exemple, pour \(n=4\) :

\(N_(10)\)	\(N_(2)\)	\(\bar{N}_(2)\)	\(-N_(2)\)	\(-N_(10)\)
0	0000	1111	0000	0
1	0001	1110	1111	-1
2	0010	1101	1110	-2
3	0011	1100	1101	-3
4	0100	1011	1100	-4
5	0101	1010	1011	-5
6	0110	1001	1010	-6
7	0111	1000	1001	-7
			1000	-8

On peut ainsi représenter des nombres compris entre -4 et +3 sur un format de 4 bits, entre -16 et +15 sur un format de 5 bits, entre -32 et +31 sur un format de 6 bits, entre -64 et +63 sur un format de 7 bits, etc.

Note

• Le bit de poids fort (MSB) est représentatif du bit de signe, mais il est traité comme les autres bits dans les opérations arithmétiques : si MSB = 0 le nombre est positif, si MSB = 1 le nombre est négatif.
• Le nombre \(+2^{n-1}\) n’est pas représenté. En effet, dans le cas où \(n=4\), le calcul du CA2 de 1000 donne \(-(-8) = 0111 + 1 = 1000 = -8\). Ce qui est arithmétiquement incorrect, car \(0\) est le seul entier à être son propre opposé. On a donc choisi de supprimer la représentation du nombre \(+2^{n-1}\) , un MSB à 1 étant représentatif d’un nombre négatif.

Codage virgule fixe pour les nombres réels signés

Dans la représentation virgule fixe, les nombres réels sont représentés par des entiers, après avoir décidé d’un facteur d’échelle \(k\) qui est une puissance de la base dans laquelle on écrit les entiers. Autrement dit, un bloc de \(n\) bits est considéré comme un nombre dont la partie entière et le signe sont codés sur \(n-k\) bits, et dont la partie fractionnaire est codée sur \(k\) bits. La résolution d’une telle représentation est de \(2^{-k}\) . L’addition de deux nombres réels en virgule fixe (s’ils possèdent le même facteur d’échelle k) revient à additionner les deux entiers qui représentent ces nombres. Ce codage est surtout utilisé dans les processeurs de traitement de signal (DSP) où les exigences de rapidité sont primordiales. En revanche, la dynamique de cette représentation est assez limitée : pour un format sur \(n\) bits avec \(k\) bits après la virgule, la dynamique est de \((2^n-1)/2^k\) .

Exemple pour des nombres sur 8 bits dont 4 bits de partie entière

La virgule est positionnée uniquement afin de faciliter la lecture. Elle n'est pas présente dans la machine, ni dans la description VHDL.

Nombre réel signé	Nombre codé sur 8 bits dont 4 bits de partie entière
+3	0011,0000
+2,5	0010,1000
+2	0010,0000
+1,5	0001,1000
-1,5	1110,1000
-2	1110,0000
-2,5	1101,1000
-3	1101,0000